Data Structures
What are data?
Data (and their various types) are the basic building blocks of programming.
They represent a unit or element of information that can be accessed through an identifier - for example, a variable.
Most programming languages work with variations based on the four primitive types below:
- INT or integer: whole numeric values (positive or negative);
- FLOAT or "floating point": numeric values with decimal places (positive or negative);
- BOOLEAN or booleans: represented by only two values, "true" and "false". Also called logical operators;
- TEXT or character strings: sequences or chains of characters, used to manipulate text and/or other non-numeric or boolean data types, such as cryptographic hashes.
JavaScript, for example, has built-in primitive types in its basic language structure: number, string, boolean, and symbol (for "symbolic name", used among other things to create unique properties in objects). C# (C-Sharp) works with a larger number of primitive types, according to the memory space that will be occupied by the variable: Boolean, Byte, SByte, Int16, UInt16, Int32, UInt32, Int64, UInt64, IntPtr, UIntPtr, Char, Double, and Single. C, on the other hand, doesn't have its own boolean data type; false is represented by the number 0 and any other digit represents true. Other languages may work with other variations.
Characteristics
Each data structure has its own set of methods to perform operations such as:
- ⬆️ Insert or delete elements;
- 🔎 Search and locate elements;
- 🔄 Sort (classify) elements according to some specified order.
Types:
- 📦 Array
- 📦 Linked List
- 📦 Stack
- 📦 Queue
- 📦 Tree
- 📦 Graph
- 📦 Hash Table
- 📦 Heap
- 📦 Trie
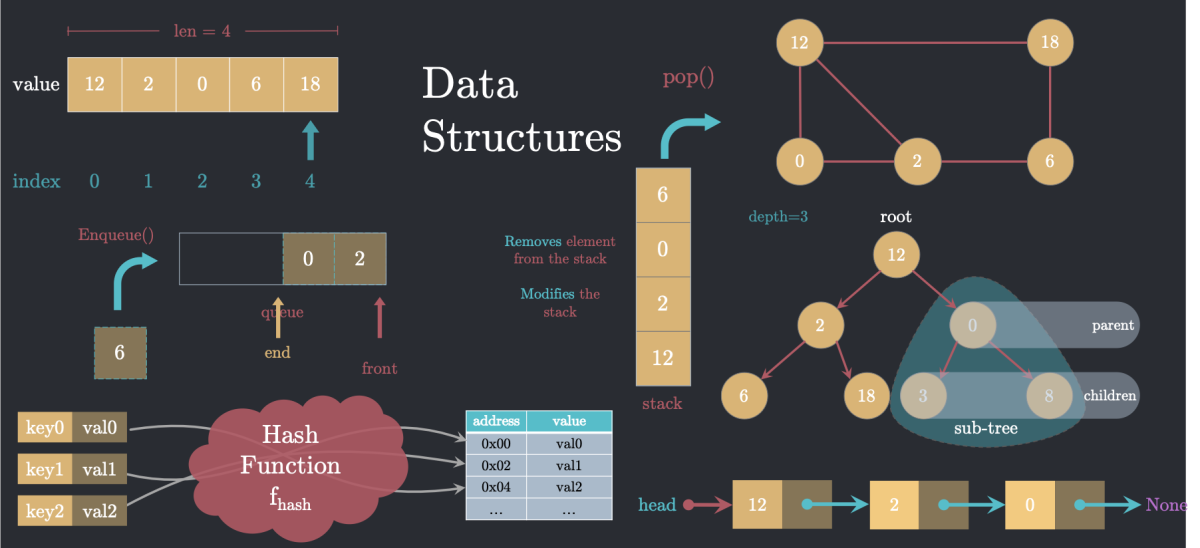
Array
An array is a linear data structure that stores a collection of elements in a single variable. The elements are stored sequentially, one next to the other, and can be accessed through an index. They don't change position, but can be removed or added. They are of the same data type.
const array = [1, 2, 3, 4, 5];
array[0]; // 1
array[1]; // 2
array[2]; // 3
array.push(6); // [1, 2, 3, 4, 5, 6]
array.pop(); // [1, 2, 3, 4, 5]
array.shift(); // [2, 3, 4, 5]
array.unshift(1); // [1, 2, 3, 4, 5]
Linked List
A linked list is a linear data structure that stores a collection of elements in a single variable.
const linkedList = [1, 2, 3, 4, 5];
linkedList[0]; // 1
linkedList[1]; // 2
linkedList[2]; // 3
linkedList.push(6); // [1, 2, 3, 4, 5, 6]
linkedList.pop(); // [1, 2, 3, 4, 5]
linkedList.shift(); // [2, 3, 4, 5]
linkedList.unshift(1); // [1, 2, 3, 4, 5]
Stack
A stack is a linear data structure that stores a collection of elements in a single variable.
const stack = [1, 2, 3, 4, 5];
stack[0]; // 1
stack[1]; // 2
stack[2]; // 3
stack.push(6); // [1, 2, 3, 4, 5, 6]
stack.pop(); // [1, 2, 3, 4, 5]
stack.shift(); // [2, 3, 4, 5]
stack.unshift(1); // [1, 2, 3, 4, 5]
Queue
A queue is a linear data structure that stores a collection of elements in a single variable.
const queue = [1, 2, 3, 4, 5];
queue[0]; // 1
queue[1]; // 2
queue[2]; // 3
queue.push(6); // [1, 2, 3, 4, 5, 6]
queue.pop(); // [1, 2, 3, 4, 5]
queue.shift(); // [2, 3, 4, 5]
queue.unshift(1); // [1, 2, 3, 4, 5]
Tree
A tree is a non-linear hierarchical data structure consisting of nodes connected by edges. Each tree has:
- A root node
- Parent and child nodes
- Leaf nodes that have no children
class TreeNode:
def __init__(self, value):
self.value = value
self.children = []
def add_child(self, child):
self.children.append(child)
# Usage example
root = TreeNode("A")
child1 = TreeNode("B")
child2 = TreeNode("C")
root.add_child(child1)
root.add_child(child2)
child1.add_child(TreeNode("D"))
child1.add_child(TreeNode("E"))
Use cases
- Representation of hierarchies (file systems)
- Decision trees in AI
- Expression trees in compilers
- Data organization (binary search trees)
Complexity
Access: O(log n) for balanced trees, O(n) in worst case Insertion: O(log n) for balanced trees, O(n) in worst case Search: O(log n) for balanced trees, O(n) in worst case Deletion: O(log n) for balanced trees, O(n) in worst case
Graph
A graph is a non-linear data structure consisting of a set of vertices (nodes) connected by edges. Graphs can be directed (edges with direction) or undirected.
class Graph:
def __init__(self):
self.graph = {}
def add_vertex(self, vertex):
if vertex not in self.graph:
self.graph[vertex] = []
def add_edge(self, source, destination):
if source in self.graph:
self.graph[source].append(destination)
else:
self.graph[source] = [destination]
# Usage example
g = Graph()
g.add_vertex("A")
g.add_vertex("B")
g.add_edge("A", "B")
Use cases
- Social networks
- Navigation systems
- Computer networks
- Maps and routes
Complexity
- Access: O(V + E), where V is the number of vertices and E is the number of edges
- Insertion: O(1)
- Search: O(V + E)
- Deletion: O(V + E)
Hash Table
A hash table is a data structure that implements an associative array, mapping keys to values. It uses a hash function to calculate an index where the value will be stored.
const hashTable = new Map();
// Inserting values
hashTable.set("key1", "value1");
hashTable.set("key2", "value2");
// Accessing values
console.log(hashTable.get("key1")); // "value1"
// Removing values
hashTable.delete("key1");
Use cases
- Caches
- Databases
- Dictionaries
- Symbol tables in compilers
Complexity
- Access: O(1) on average, O(n) in worst case
- Insertion: O(1) on average, O(n) in worst case
- Search: O(1) on average, O(n) in worst case
- Deletion: O(1) on average, O(n) in worst case
Heap
A heap is a tree-based data structure that satisfies the heap property. In a max heap, each parent node is greater than or equal to its children; in a min heap, each parent node is less than or equal to its children.
import heapq
# Creating a min heap
heap = []
heapq.heappush(heap, 5)
heapq.heappush(heap, 2)
heapq.heappush(heap, 8)
# Removing the smallest element
smallest = heapq.heappop(heap) # 2
Use cases
- Priority queues
- Sorting algorithms (Heapsort)
- Shortest path algorithms
- Memory management
Complexity
- Access to max/min: O(1)
- Insertion: O(log n)
- Deletion: O(log n)
- Construction: O(n)
Trie (Prefix Tree)
A trie is a tree data structure used to store strings. Each node represents a character, and the paths from the root to the leaf nodes form strings.
class TrieNode:
def __init__(self):
self.children = {}
self.end_of_word = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
node = self.root
for char in word:
if char not in node.children:
node.children[char] = TrieNode()
node = node.children[char]
node.end_of_word = True
Use cases
- Autocomplete
- Spell checking
- Dictionaries
- IP routing
Complexity
- Insertion: O(m), where m is the length of the string
- Search: O(m)
- Deletion: O(m)
Conclusion
Data Structures and Algorithms are the core of software development and are exactly where you should start if you want to learn programming. Each data structure has a case where it is best used. Choosing the right data structure can significantly impact the performance and maintainability of an application.
It's important to understand the time and space complexities of each structure, as well as their ideal use cases. By mastering these structures, you'll be better equipped to solve complex problems and optimize your solutions.
Remember that practice is essential to internalize these concepts. Try implementing these structures in your programming language and solve practical problems using them - I recommend doing some Leetcode. Over time, you'll develop a natural intuition for choosing the most appropriate data structure for each situation.